浦和明の星女子中学校・2026年算数 解説【完答編】
こんにちは。
スタディーズラボの上田です。
完答編では最終問を解くためにしなければいけない思考を活用して解いていきます。
目次
クリック/タップでジャンプします。
大問1
(1) ~ (6)
合格編へ。
(7) ①
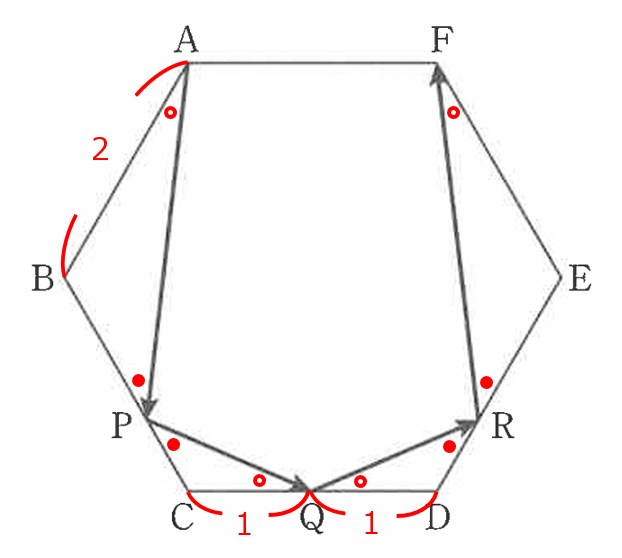
誘導にあるように反射前後で角度が同じことを利用すると、図の4つの三角形は全て相似だとわかります。
CQ:QD は左右対称なので 1:1 より、BP:PC = 2:1。
(7) ②
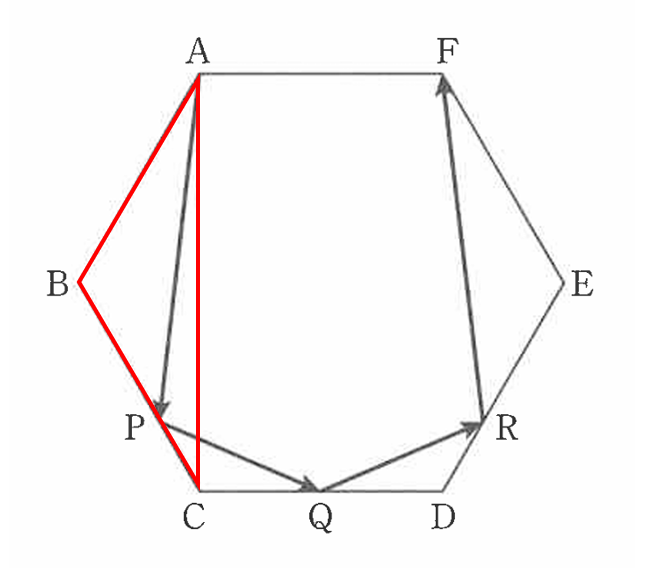
赤く囲った三角形の面積は六角形の面積の $\dfrac{1}{6}$倍のため、△ABPの面積は底辺の比より、$\dfrac{1}{6}$ × $\dfrac{2}{3}$ = $\dfrac{1}{9}$倍。△FERの面積も同じ。
△QCPは△ABPと 1:2 の相似なので、面積比は 1:4。よって六角形の面積の $\dfrac{1}{9}$ × $\dfrac{1}{4}$ = $\dfrac{1}{36}$倍。△QDRも同じ。
五角形APQRFの面積は六角形から三角形 4つ引けばいいので、1 – $\dfrac{1}{9}$ × 2 – $\dfrac{1}{36}$ × 2 = $\dfrac{13}{18}$
よって、1:$\dfrac{13}{18}$ = 18:13。
大問2
大問3
(1)
グラフの最後、45分のタイミングで出会っていること、それが2回目であることに注目します。
異なる出発地点から出発して2回で会うまでに、二人で合計片道3本分移動しています。
線分図を描くとわかりやすいです。
同様に考えると、1回出会うまでに、二人で合計片道1本分移動しています。
かかる時間も 1:3 なので、45 ÷ 3 = 15分。
(2) (3)
二人の間の距離のグラフをダイヤグラムに書き換えます。
大問4
(1)
大きい箱、小さい箱の2種類混ざっていて難しく見えますが、”大きい箱と小さい箱の比が常に 2:1″ になっていることに注目します。
イメージとして、とても大きな箱に大箱 × 2 と小箱 × 1 を詰めていくことにします。
詰め直した後は、ミカンがとても大きな箱 9箱にいっぱいに入り 101個余り、とても大きな箱12箱をいっぱいにするには25個足りませんでした。と、読み替えることができます。
あとは差に注目して、とても大きな箱 3箱には 101 + 25 = 126個入る、1箱には 126 ÷ 3 = 42個入る、とわかります。
9箱と余りが101個出るので、 42 × 9 + 101 = 479個。
(2)
とても大きな箱 1つには 126 ÷ 3 = 42個入ります。
これをもとにそれぞれを絞っていきます。
大箱は余った 101個のミカンを 6箱では詰め切れないので、1箱 101 ÷ 6 = 16.いくつか… 16個以下。
小箱は足りなかった25個のミカンを2箱では詰め切れないので、1箱 25 ÷ 2 = 12.いくつか… 12個以下。
とても大きな箱には大箱 × 2 と小箱 × 1 入っていたので、上の条件を満たしつつ、この 3箱で 42個にする組み合わせを調べます。
( 大箱, 小箱 ) = ( 16個, 10個 ), ( 15個, 12個 ) が見つかるはずです。
大問5
(1) ①
試行錯誤していると、左から順に埋めていくとき、5回増やして、1回だけ減らすしかないということに気づきます。
6回の試行中、1回だけ減らすので、6通り。
(1) ②
考え方は全く同じです。
99回増えるか減るかの試行があるので、99通り。
(2) ①
(1) ② から 1回増減の試行が増えるだけです。( 1行目 1番目 → 2行目 1番目。この後は (1) ② と同じ。)
99 + 1 = 100通り。
(2) ②
法則としては 1行目がいつ減るか、で 2行目の並び方が何通りあるかが変化します。
100 × 2 の場合、最後に減らせば 100通り、最後から2番目に減らせば 99通り…となるので、
2 ~ 100 を全部足したものが答えとなります。(なぜ 1 を入れないかというと、1行目の最初の増減の試行で減らしても、2行目 1番目は 0 と 2 の両方があり得るからです。)
( 2 + 100 ) × 99 ÷ 2 = 5049通り。
なぜ 1 を入れないか、は文章で説明されるより、自分で小さな表を作って試行錯誤して見つけてほしいです。
私は 4 × 2 程度の小さな表を作って試行錯誤しました。
完全に再現した試行錯誤以外もしていいんだ!という気づきはほかの問題に生きてきます。

