浦和明の星女子中学校・2026年算数 解説【合格編】
こんにちは。
スタディーズラボの上田です。
今回は合格編ということで、基礎的な問題や、大問の(1)に絞って解説します。
また、あえて泥臭い解き方をします。
それができることも合格のために大事な力だと考えています。
完答編では完答するために必要な法則を用いてここで解説済みの問題含めて解説します。
完答できる能力がある場合、より速い解き方を知ってほしいからです。
目次
クリック/タップでジャンプします。
大問1
(1)
(3$\dfrac{1}{4}$ × 3.96 + 4.55 × 0.4 – 1.33 ÷ 2$\dfrac{1}{2}$) × 2.5 – 4$\dfrac{2}{3}$ ÷ 3$\dfrac{1}{3}$ × $\dfrac{13}{14}$
= (12.87 + 1.82 – 0.57) × 2.5 – 1.3
= 34
分数の掛け算割り算の約分をした時点で全て小数にできます。すべて小数にできた場合、小数は通分の必要がないので計算ミスを減らしやすいです。
問題によって柔軟に使い分けられると◎。
(2)
$\dfrac{1}{□}$ が□番目の三角数番目にあることに注目。$\dfrac{1}{12}$ があるのは12番目の三角数で 1 + 2 + 3 + … + 12 = (1 + 12) × 12 ÷ 2 = 78番目。$\dfrac{5}{12}$はその4つ前なので 78 – 4 = 74番目。
(3)
まずは2つの水槽の重さの差から水の重さを計算します。
重さの差の 6.1 – 5.3 = 0.8kg は、容積の $\dfrac{4}{5}$ – $\dfrac{2}{3}$ = $\dfrac{2}{15}$ に当たるので、最大まで水を入れたときの重さは 0.8 ÷ $\dfrac{2}{15}$ = 6kg。 よって、5.3 – 6 × $\dfrac{2}{3}$ = 1.3kgが水槽の重さとわかります。
(4)
定価は400 × 1.25 = 500円、割引後は 500 – 500 × 0.1 = 450円。売れたときの利益はそれぞれ、100円、50円。
全て定価で売れたときの利益が 15000 ÷ $\dfrac{3}{5}$ = 25000円なので、仕入れた個数は 25000 ÷ 100 = 250個。
これをつるかめ算で解いていきます。
250個すべてが定価で売れたときの利益は25000円と実際より10000円多い。ひとつ値引きして売るごとに50円利益が減るから、割引したのは 10000 ÷ 50 = 200個。定価で売れたのは、250 – 200 = 50個。
(5)
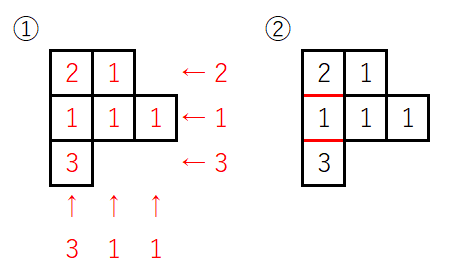
①
正面から見た図からタテは右から3, 1, 1。右から見た図からヨコは上から2, 1, 3。
図の赤色のようにその場所には何段重なっているかという数字を書き込む。
全部足して、9個。
②
①の数字を活用しながら考えます。
表面積の求め方として、全方向から見える面積の合計を出すという方法があるのですが、今回はそれを使うと数えきれない部分があります。
図②の赤で示した部分です。そこだけ別枠で計算します。
上下から見た面積(6 × 2) + 正面背後から見た面積(5 × 2) + 左右から見た面積(6 × 2) + 赤の部分の面積 ( 2 ) = 36面。
1面 1cm²だから、36 × 1 = 36cm²。
(6)
大小関係から、
A:1□□、B:2□□、C:3□□、D:4□□、E:5□□
(Dが5の倍数であることからDの1の位を埋めてもいいです。埋めなくても②まで解けます。)
3桁の81の倍数は、順に162、243、324、405、486、567、… となり、1~5のみを使ってできるのが243、324のちょうど2つなので、B、Cが確定します。
A:1□□、B:243、C:324、D:4□5、E:5□□ …ここまでで ①
この時点で1の位に使える数字は1と2、10の位は1、3、5。これとEからAを引くと359になることから虫食い算を作って解きます。
それぞれ使える数字が少ないので比較的すぐに解けると思います。
A:152、E:511 … ②
(7)
大問2
基礎的な操作で完答できるので、ここで(3)まで解説します。
(1)
てんびん図がおすすめです。
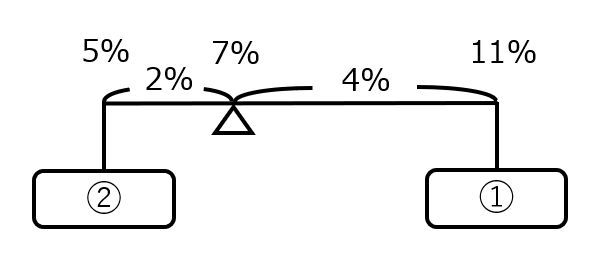
A:5%ー①ー7%ー②ー11%:C
より重さが
A:C = ②:①、② = 300g なので、Cの重さは、 ① = 300 ÷ 2 = 150g。
(2)
200g入れたことになるので、全体の重さが 300 + 200 = 500g、塩の重さが 300 × 0.05 + 200 × 0.11 = 37g。
濃さは、 37 ÷ 500 × 100 = 7.4%。
(3)
Bを270g入れると、全体の重さが 500 + 270 = 770g、塩の重さが 37 + 270 × 0.06 = 53.2g。
塩の重さを変えずに濃さを 7%にするので、塩と濃さから目指すべき全体の重さを計算します。
□ × 0.07 = 53.2
□ = 760g
目指すべき重さが 760gとわかったので、蒸発した水の重さは、770 – 760 = 10g。
大問3
(1)
グラフの最後、45分のタイミングで出会っていること、それが2回目であることに注目します。
異なる出発地点から出発して2回で会うまでに、二人で合計片道3本分移動しています。
線分図を描くとわかりやすいです。
同様に考えると、1回出会うまでに、二人で合計片道1本分移動しています。
かかる時間も 1:3 なので、45 ÷ 3 = 15分。
(2)
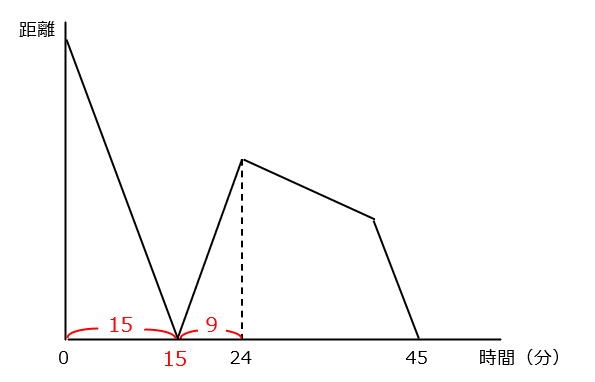
花子さんが”太郎さんと出会うまでの15分”に進んだ距離を、太郎さんは 9分で進んでいるから、
その距離を進むのにかかる時間の比が 太郎:花子 = 3:5。
同じ距離をすすむのにかかる時間と速さは逆比の関係だから、5:3。
(3)
完答編へ。
大問4
(1)
大きい箱、小さい箱の2種類混ざっていて難しく見えますが、”大きい箱と小さい箱の比が常に 2:1″ になっていることに注目します。
イメージとして、とても大きな箱に大箱 × 2 と小箱 × 1 を詰めていくことにします。
詰め直した後は、ミカンがとても大きな箱 9箱にいっぱいに入り 101個余り、とても大きな箱12箱をいっぱいにするには25個足りませんでした。と、読み替えることができます。
あとは差に注目して、とても大きな箱 3箱には 101 + 25 = 126個入る、1箱には 126 ÷ 3 = 42個入る、とわかります。
9箱と余りが101個出るので、 42 × 9 + 101 = 479個。
(2)
完答編へ。
大問5
(1) ①
いきなりスマートに解くのではなく、規則の最初の問題は試行錯誤をさせる問題だと考えてください。
以下を漏れなく見つけ出せれば正解です。
(1) 2 3 4 5 6 (5)
(1) 2 3 4 5 4 (5)
(1) 2 3 4 3 4 (5)
(1) 2 3 2 3 4 (5)
(1) 2 1 2 3 4 (5)
(1) 0 1 2 3 4 (5) …6通り。
(1) ②
この先は数え上げはほぼ不可能です。
どうでしょう。
①を見て法則性に気づきましたか?
答え合わせは完答編へ。

